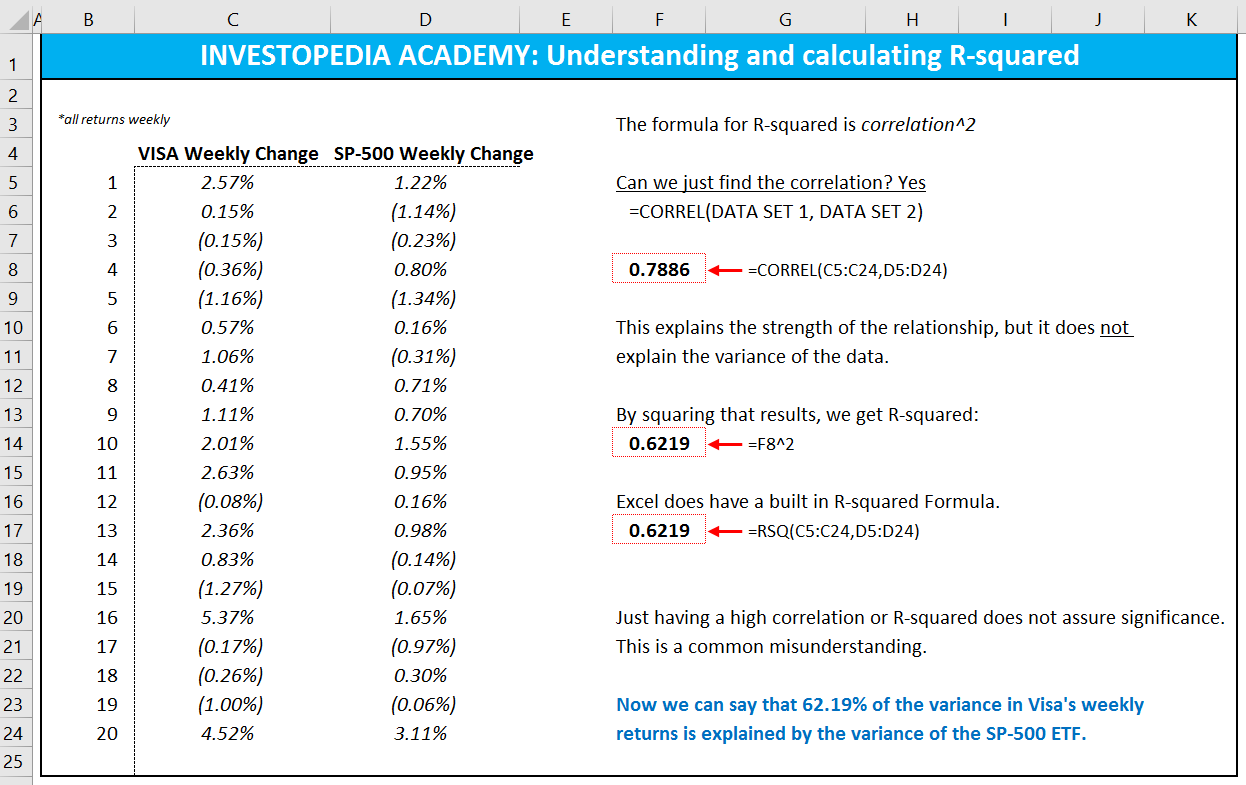
We can add 100 different variables to a model and probably the predictive power of the model will be outstanding. We are trying to use a few independent variables that approximately predict the result. The trade-off is complex, but simplicity is better rewarded than higher explanatory power. R-squared (R2) is defined as a number that tells you how well the independent variable(s) in a statistical model explains the variation in the dependent variable.
R-Squared: Definition and How to Calculate
Its interpretation in clinical medicine is very context-dependent and lacks a definitive threshold. What measure of yourmodel’s explanatory power should you report to your boss or client orinstructor? You should more strongly emphasize the standard error of the regression,though, because that measures the predictive accuracy of the model in realterms, and it scales the width of all confidence intervals calculated from themodel. You may also want to reportother practical measures of error size such as the mean absolute error or meanabsolute percentage error and/or mean absolute scaled error.
Introduction to Statistics Course
Because the dependent variables are notthe same, it is not appropriate to do a head-to-head comparison of R-squared. Arguably this is a better model, becauseit separates out the real growth in sales from the inflationary growth, andalso because the errors have a more consistent variance over time. (The latter issue is not the bottomline, but it is a step in the direction of fixing the model assumptions.) Most interestingly, the deflated incomedata shows some fine detail that matches up with similar patterns in the salesdata. However, the error varianceis still a long way from being constant over the full two-and-a-half decades, andthe problems of badly autocorrelated errors and a particularly bad fit to themost recent data have not been solved. To sum up, the R-squared basically tells us how much of our data’s variability is explained by the regression line. When we feel like we are missing important information, we can simply add more factors.
Properties and interpretation
With a multiple regression made up of several independent variables, the R-squared must be adjusted. The reason why many misconceptions about R² arise is that this metric is often first introduced in the context of linear regression and with a focus on inference rather than prediction. Understanding the limitations of the R2 value in clinical medicine is critical. how do you interpret r squared Medical outcomes are most often formed as a culmination of numerous complex factors, and relying solely on an R2 value could oversimplify these non-linear relationships. Adjusted R-squared isonly 0.788 for this model, which is worse, right? Well, no. We “explained” some of the variancein the original data by deflating it prior to fitting this model.
Using R-squared to Compare Different Models
Statisticians call this specification bias, and it is caused by an underspecified model. For this type of bias, you can fix the residuals by adding the proper terms to the model. A value of 1 indicates that the explanatory variables can perfectly explain the variance in the response variable and a value of 0 indicates that the explanatory variables have no ability to explain the variance in the response variable. The second model only has a higher R-squared value because it has more predictor variables than the first model.
- If you are looking for a widely-used measure that describes how powerful a regression is, the R-squared will be your cup of tea.
- However, the predictor variable that we added (shoe size) was a poor predictor of final exam score, so the adjusted R-squared value penalized the model for adding this predictor variable.
- There is one more consideration concerning the removal of variables from a model.
- Techniques like variance inflation factor analysis or principal component analysis can help identify and mitigate multicollinearity.
- In fact, R² values for the training set are, at least, non-negative (and, in the case of the linear model, very close to the R² of the true model on the test data).
That is, the standard deviation of theregression model’s errors is about 1/3 the size of the standard deviationof the errors that you would get with a constant-only model. That’s very good, but itdoesn’t sound quite as impressive as “NINETY PERCENTEXPLAINED! If you use Excelin your work or in your teaching to any extent, you should check out the latestrelease of RegressIt, a free Excel add-in for linear and logistic regression.See it at regressit.com.
Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more. What qualifies as a “good” R-squared value will depend on the context. In some fields, such as the social sciences, even a relatively low R-squared value, such as 0.5, could be considered relatively strong. In other fields, the standards for a good R-squared reading can be much higher, such as 0.9 or above. In finance, an R-squared above 0.7 would generally be seen as showing a high level of correlation, whereas a measure below 0.4 would show a low correlation.
If the model is sensible in terms of its causal assumptions, then there is a good chance that this model is accurate enough to make its owner very rich. Statology Study is the ultimate online statistics study guide that helps you study and practice all of the core concepts taught in any elementary statistics course and makes your life so much easier as a student. Fortunately there is an alternative to R-squared known as adjusted R-squared. The degrees-of-freedom adjustment allows us to take this fact into consideration and to avoid under-estimating the variance of the error terms.
This is because the model essentially captures noise or random fluctuations in the training data, rather than underlying patterns or relationships. These approaches help ensure that the model captures general trends rather than specific quirks of the training data, improving its generalizability to unseen data. Now, what is the relevant variance that requiresexplanation, and how much or how little explanation is necessary or useful?
